Binary Search Algorithms, Flowchart in c
A binary search is an efficient algorithm used to search for a specific value within a sorted collection of data. To eliminate the fraction of the data that cannot contain the required value, the search space is cut in half periodically.
Table of Contents
The binary search algorithm follows these steps:
- Start with the entire sorted collection of data.
- Compare the target value with the middle element of the collection.
- The search is complete if the target value is equal to the central element.
- If the target value is less than the central element, the search continues on the lower half of the collection.
- If the target value exceeds the central part, the search continues on the upper half of the collection.
- Repeat steps 2-5 until the target value is found or the search space is empty.
Explain the binary search with an algorithm.
- Binary search is an efficient search as compared to a linear search. it is used to search elements from a sorted array.
- In the search middle element of an array is compared with the item, if they are equal then a search is successful.
- Otherwise, if item > middle element then perform searching in the upper half or if item<middle element then perform searching in the lower half.
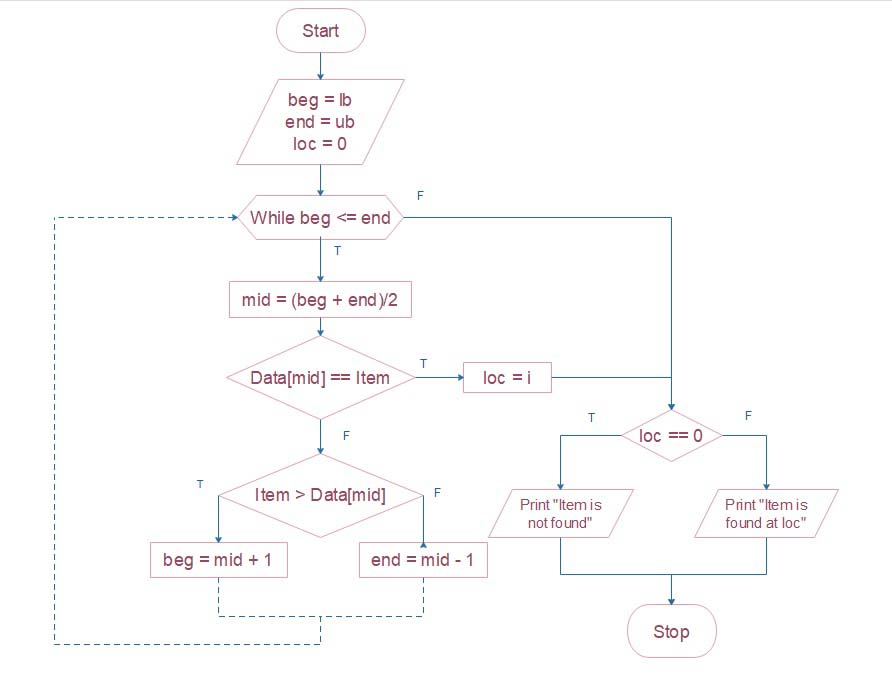
Here binary search flowchart
Working Binary Search
- Initially set beg = 1 and end = size of the array, then find the middle of an array using mid= (beg+end)/2.
- Compare array[mid] with the item to be searched, if they are equal the search is successful and the process is stopped.
- When the value of item > array[mid] then proceed to search in the upper half using beg = mid + 1. Otherwise, when the value of item < array [mid] then proceeds to search in the lower half using end = mid – 1.
- The same steps are repeated in the respective half until the element is found or beg <= end.
Algorithm: Binary_Serach[Data[], lb, ub, item, loc]
- This is the algorithm for linear search
- Data[]- Array of an element,
- lb-lower bound,
- ub-upper bound,
- beg-beginning position,
- end-end position,
- mid-middle position,
- item-element to be searched,
- loc-location.
Binary Search in c
step 1: start
step 2 : [initialize variable]
Set beg=lb, end=ub,loc=0
step 3 : Repeat steps4, 5 and 6 until beg <= end and data[mid] != item
step 4 : [find middle]
mid=(beg+end)/2
step 5 : [compare data[mid] and item]
if data [mid] == item the
set loc=mid
End if
step 6 : [jump in respective half]
if item >data[mid]then
beg = mid + 1
else
end = mid-1
step 7 : if loc == 0 then
Print "item is not found"
else
Print "item is found at loc"
step 8 : StopExample Binary Search
Consider the following example containing 8sorted array elements.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 |
The element to be searched is: 55
set
beg = 1 and
end = 8
Pass 1
Find mid
mid = (ben+end)/2
mid = (1+8)/2
mid = 4
compare A[mid] with 55
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 |
Red is mid
As A[mid] != 55 &
55 > A[mid] Proceed searching in the Upper half
Set beg = mid + 1
beg = 4 + 1
beg = 5
Pass 2
Find mid
mid = (beg+end)/2
mid = (5+8)/2
mid = 6
compare A[mid] with55
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 11 | 22 | 33 | 5 | 55 | 66 | 77 | 88 |
Red is mid
As A[mid] != 55 &
55 < A[mid] Proceed searching in the lower half
Set end = mid-1
end = 6 – 1
end = 5
Pass 3
Find mid
mid = (beg+end)/2
mid = (5+5)/2
mid = 5
compareA[mid] with 55
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 |
Red is mid
As A[mid] = 55
Print “Search is Successful”
Result: Given element 55 is found at the 5th position
Given that the size of the input data, n, determines the temporal complexity of an algorithm, the binary search algorithm is particularly significant. As a result, the search time increases logarithmically as the size of the data set increases. The temporal complexity of a straightforward linear search, in contrast, is O(n), and the search time scales linearly with the quantity of the data.
Binary search is very useful for huge data sets when short search times are essential due to its efficiency. It is frequently used in a variety of applications, including looking for a certain value in a binary search tree, searching for an element in a sorted array, and using an index to find something in a database.
Binary search lowers the number of comparisons needed to discover the target value by halving the search space at each stage. When working with huge datasets or conducting several searches, this efficiency is very beneficial. It enables quicker information retrieval and enhances overall performance across various computer science and software engineering jobs.
Binary Search FAQs
Can binary search be used on unsorted data?
No, binary search requires the data to be sorted in ascending or descending order for it to work correctly. If the data is unsorted, the algorithm may give incorrect results.
What happens if the target value is not present in the data?
If the target value is not found during the binary search, the algorithm will eventually narrow down the search space until there are no more elements left. At that point, it will conclude that the target value is not present in the data.
Is binary search only applicable to arrays?
No, binary search can be used on other data structures as well, such as sorted lists or binary search trees. As long as the data is sorted, binary search can be applied.
How does binary search compare to linear search?
Binary search is generally more efficient than linear search, especially for large data sets. Linear search checks each element one by one until it finds the target value or reaches the end of the data. Binary search, on the other hand, eliminates half of the remaining search space at each step, resulting in faster search times.
What is the worst-case time complexity of binary search?
The worst-case time complexity of the binary search is O(log n), where n is the size of the data set. This means that the search time grows logarithmically with the size of the data, making it highly efficient.
Can binary search be used on non-numeric data?
Yes, binary search can be applied to non-numeric data as long as it is sorted based on a defined order. For example, if you have a sorted array of strings, you can perform a binary search to find a specific string within the array.